1004번: 어린 왕자
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 첫째 줄에 출발점 (x1, y1)과 도착점 (x2, y2)이 주어진다. 두 번째 줄에는 행성계의 개수 n이 주
www.acmicpc.net
1. 문제 이해
1004번 문제, "어린 왕자"는 주어지는 원들의 정보(반지름, 중심 좌표)를 활용해서, 특정 원의 내부에서부터 다른 어떤 원의 내부까지 이동할 때 경계를 몇 번 거쳐야 하는가를 찾는 문제이다.

문제에서는 위와 같은 그림을 제시한다.
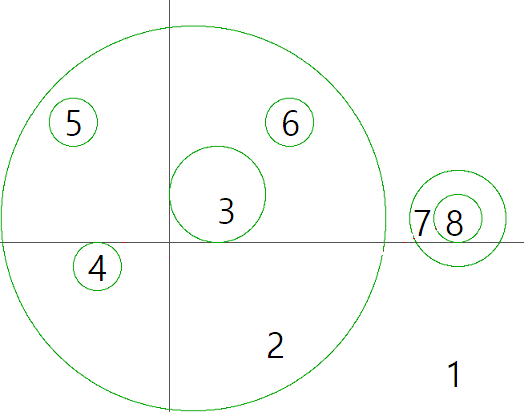
그림에서 보이는 각각의 원들에 번호를 붙여 보았다. 바깥의 1번은, 보이지 않는 무한히 큰 원이 하나 있다고 가정한 것이다. 하나의 원에서 다른 원으로 이동할 때 한 번 경계를 거치며, 위 그림에서 자신이 2번에 있다면 한 번 움직여서 갈 수 있는 원은 1(바깥), 3, 4, 5, 6번이다. 움직일 수 있는 경로를 선으로 나타내 보면 다음과 같아진다.

마치 1번을 루트 노드로 가지는 트리의 형태로 보이기도 하나 우주선이 움직일 수 있는 방향에는 제한이 없으므로 무지향성 그래프라고 보고 푸는 것이 합리적이다. 이때 특정 원에서 다른 원까지 이동할 때 필요한 최소 경계 통과 횟수, 즉 도착지까지 원을 최소 몇 번 이동해야 하는가를 구해야 하므로 주어진 출발 위치가 속한 원을 시작으로 탐색 알고리즘을 활용하여 최소 횟수를 얻어내야 한다.
정점(원)을 잇는 간선(위 사진의 붉은 색 선)에 가중치가 없으며, 최단 거리를 찾는 문제이므로 BFS를 활용하는 것이 바람직하다고 판단하였다.
2. BFS란?
BFS(Breadth First Search, 너비 우선 탐색) 알고리즘은 그래프에서 한 정점에 인접한 모든 정점을 방문해 가면서 그래프를 탐색하는 방식이다.
1번이 출발 지점일 때 방문 순서는 위 사진의 각 정점에 적힌 숫자와 같다. 트리와 같이 나타낸 위의 형태에서는 마치 같은 depth의 정점들을 우선하여 방문하는 것으로 보여 너비 우선 탐색이라 한다. 꼭 트리의 형태여야 하는 것은 아니다. 위 사진의 정점들이 트리의 형태로, 아래 방향으로 가듯 정렬되어 있지만 1번이 출발점이라는 것과 연결된 정점만 같다면, 예를 들어 2번과 4번 노드가 1보다 높은 곳에 그려져 있다고 하더라도 방문 순서는 같다. 인접한 정점을 우선으로 방문한다고만 기억하면 된다. 이 때, 한 번 방문한 정점은 다시 방문하지 않는다.
BFS와는 다르게 일단 다다를 수 있는 마지막(가장 깊이 있는) 정점까지 가 본 후에 찾는 정점이 아닐 때 다시 돌아와서 다른 정점을 방문하고, 또 아니라면 돌아가서 다른 정점을 방문하는 DFS(Depth First Search, 깊이 우선 탐색)이라는 방식이 있다. 본 문제에서는 DFS에 비해 최단 거리를 구하기 더욱 용이하고 무지향성 그래프에서 Cycle이 생기더라도 안정적으로 탐색을 수행할 수 있는 BFS를 선택하는 것이 합리적이라고 판단된다.
BFS를 구현하는 방식으로 큐(Queue)를 활용하는 것을 꼽을 수 있다. 큐는 대표적인 선입선출(FIFO, First In First Out) 구조의 자료형이다. 쉽게 말하자면, "큐"라는 저장 공간에는 여러 개의 데이터를 담을 수 있는데, 이후 데이터를 삭제할 때는 데이터가 추가된 순서대로 삭제된다. 마치 놀이공원의 줄처럼, 먼저 줄을 선 사람이 먼저 들어가는 것과 같다. 데이터를 맨 뒤에 삽입하는 과정을 enqueue(C++ STL에서는 push), 맨 앞의 데이터를 제거하는 과정을 dequeue(C++ STL에서는 pop)이라고 한다.

이를 이용해 위 그래프를 예시로 문제를 해결하는 과정은 다음과 같다.

출발 지점이 2, 도착 지점이 8이라고 가정하자.
우선 빈 큐 하나를 생성하여 출발 지점을 담는다.
Queue: [2]
Queue의 맨 앞의 데이터는 2이다. 이때 2에 인접한 정점은 1, 3, 4, 5, 6이다. 2를 방문했다고 기록한 뒤 1, 3, 4, 5, 6을 큐에 넣는다.
Queue: [2, 1, 3, 4, 5, 6]
현재의 front()인 2를 방문했다고 기록한 후 2가 도착지점인지 확인한다. 아니라면 dequeue한 후 다음 front에 대해 위 과정을 반복한다.
Queue: (2 삭제) [1, 3, 4, 5, 6]
Queue: (1에 인접한 2(이미 방문),7 enqueue) [1, 3, 4, 5, 6, 7]
- 현재 front()가 도착지점인가? -> NO
Queue: (1 삭제) [3, 4, 5, 6, 7]
Queue: (3에 인접한 2 enqueue) [3, 4, 5, 6, 7]
- 현재 front()가 도착지점인가? -> NO
Queue: (3 삭제) [4, 5, 6, 7]
Queue: (4에 인접한 2 enqueue) [4, 5, 6, 7]
...
Queue: (7 삭제) [8]
Queue: (8에 인접한 7 enqueue) [8]
- 현재 front()가 도착지점인가? -> YES
=> 위 과정을 반복한 횟수를 반환
3. 문제에 적용
풀이 순서는 다음과 같다.
1. 정점(원)의 정보를 가지도록 그래프를 구현한다.
2. 각 원들의 간선 정보를 구한다.
3. 출발점과 도착점이 속한 원을 찾는다.
4. 주어진 출발점에서부터 BFS를 통해 최단 거리를 찾는다.
3-1
class PlanSys
{
public:
int x;
int y;
int r;
int depth;
enum class State { NOT_SEARCHING, NOT_VISITED, VISITED };
State nodeState;
vector<PlanSys*> adjacents;
PlanSys(int x_, int y_, int r_)
{
x = x_;
y = y_;
r = r_;
depth = 0;
nodeState = State::NOT_SEARCHING;
}
};
class graph
{
public:
vector<PlanSys*> nodes;
int answer;
PlanSys* departure;
PlanSys* arrival;
graph()
{
answer = 0;
AddSys(new PlanSys(0,0,9999999));
}
void AddSys(PlanSys* psys)
{
nodes.push_back(psys);
}
void AddLink(PlanSys* a, PlanSys* b)
{
if (a == NULL || b == NULL)
{
return;
}
a->adjacents.push_back(b);
b->adjacents.push_back(a);
}
};
각 정점(class PlanSys, 이름은 Planet System에서 착안)에는 원의 정보와 시작점으로부터의 거리(탐색 이전 초깃값 0), 정점의 현재 상태(탐색 중이 아님, 탐색 중이나 아직 방문하지 않음, 탐색 중이며 이미 방문하였음)를 메모할 수 있는 enum을 담았으며 인접한 정점의 포인터를 보관할 수 있도록 vector를 사용하였다.
그래프(class graph)에는 현재까지 등록한 정점, 최종적으로 출력할 정답, 출발 정점과 도착 정점의 포인터를 각각 포함하였다. graph는 기본적으로 중심이 (0,0)이고 9999999의 반지름을 가지는(무한히 큰 것으로 간주하여도 무방한) 정점을 하나 포함한다.
3-2
모든 정점이 연결된 그래프가 나와야 하므로 간선의 정보를 구해야 하나, 본 문제는 어떤 정점이 어떤 정점이 연결되어 있는지 알려주지 않는다. 그래서 직접 알아내야 한다.

작은 원을 직접 포함(원 A가 원 B를 포함할 때, 원 A에 포함되면서 원 B를 포함하는 원이 없을 때)할 때, 해당 두 원 사이를 지나갈 수 있으며 두 정점이 연결되었다고 볼 수 있다. 2번 원과 3,4,5,6번 원과의 관계가 그러하며, 7번 원과 8번 원의 관계, 1번 원과 2,7번 원의 관계가 그렇다.
가장 큰 원인 1번 원이 포함하고 있는 원은 보이는 모든 원이다. 원은 서로 교차하거나 접하지만 않을 뿐 그 이외의 경우라면 어떤 형태로든 존재할 수 있으므로 큰 원의 시점에서 본다면 어떤 원이 그 큰 원에 "직접 포함"된 원인지 구분하기 쉽지 않다. 그래서 작은 원 직접 포함하는 원을 찾는 방식으로 진행하려 한다.
중심의 좌표가 각각 (x1, y1), (x2, y2)이고 반지름이 각각 r1, r2인 두 원 A, B에 대하여, 두 원의 중심 사이의 거리를 d라고 하자. 이때 r1 > r2이다. B의 중심 좌표가 A의 둘레 내에 있으려면 d가 r1보다 작으면 된다. 즉 다음 그림과 같다.

원이 겹치는 것까지 고려하여 위치 관계를 구하면 더 엄밀하겠으나 문제에서 그러한 경우는 애초에 제시하지 않는다고 하였으므로 위와 같은 조건만으로도 충분하다. 즉 조건은
(1) r1 > r2
(2) d < r1
또한 A가 B를 직접 포함하려면
(3) A의 반지름이 B를 포함하는 원들의 반지름 중에서 최소일 것
여기서 얻은 조건으로 특정 원을 직접 포함하는 원을 구하면 다음과 같다.
class graph
{
public:
...
PlanSys* FindMinSys(PlanSys* psys)
{
PlanSys* minP = NULL;
for (PlanSys* p : nodes)
{
double d = distance(psys, p);
if (d < static_cast(p->r) && (minP == NULL || p->r < minP->r))
{
minP = p;
}
}
return minP;
}
double distance(PlanSys* a, PlanSys* b)
{
return sqrt(pow(a->x - b->x, 2) + pow(a->y - b->y, 2));
}
};
매개 변수로 받은 정점 psys과 graph에 저장된 모든 정점을 비교하여 psys를 포함하는 원을 찾는다. 이때, psys를 포함하는 원들 중 가장 작은 원을 찾으면 그것이 psys를 직접 포함하는 원이며 해당 원의 포인터를 반환한다. distance는 피타고라스 정리를 이용하여 두 원의 중심의 거리를 구하는 함수이다. 위 과정을 반지름이 9999999인 원을 제외하고 모두 수행하면 각각의 원을 직접 포함하는 원을 알 수 있으며 이들을 앞서 구현한 AddLink(PlanSys*, PlanSys*) 함수를 활용하여 연결해 주면 된다.
3-3
모든 정점을 연결하였으므로 이제 출발 지점과 도착 지점을 구하면 된다. 이때 출발점과 도착점으로 주어진 점을 직접 포함하는 원을 구해야 한다. 원이 아니라 점이지만, 위 FindMinSys(PlanSys*) 함수로 쉽게 해결할 수 있다.
위 함수는 원의 반지름과 중심간 거리를 이용해 관계를 구한다. 그런데 매개변수로 받은 psys의 반지름이 0이라면 이것을 점이라고 생각할 수 있을 것이다. 이후 main()문에서 아래와 같이 수행해 주기만 하면 된다.
graph* g = new graph();
...
g->departure = g->FindMinSys(new PlanSys(x1, y1, 0));
g->arrival = g->FindMinSys(new PlanSys(x2, y2, 0));
3-4
이제 BFS만 활용하면 된다. 나는 이를 위해 두 가지 함수를 구현하였다.
class graph
{
public:
...
void Start_BFS()
{
for (PlanSys* p : nodes)
{
p->nodeState = PlanSys::State::NOT_VISITED;
}
BFS(departure);
for (PlanSys* p : nodes)
{
p->nodeState = PlanSys::State::NOT_SEARCHING;
}
}
void BFS(PlanSys* psys)
{
queue<PlanSys*> psysQ;
psysQ.push(psys);
while (psysQ.front() != arrival)
{
psysQ.front()->nodeState = PlanSys::State::VISITED;
for (PlanSys* p : psysQ.front()->adjacents)
{
if (p->nodeState != PlanSys::State::VISITED
&& p->nodeState != PlanSys::State::NOT_SEARCHING)
{
p->depth = psysQ.front()->depth + 1;
psysQ.push(p);
}
}
psysQ.pop();
}
answer = psysQ.front()->depth;
}
};
위 코드는 [2.BFS란?]의 풀이 과정을 코드로 옮긴 것이다. 위와 같이 함수를 모두 추가하고 main을 통해 실행했을 때 코드 전문은 다음과 같다.
Fin. 코드 전문
#include
#include
#include
#include
using namespace std;
class PlanSys
{
public:
int x;
int y;
int r;
int depth;
enum class State { NOT_SEARCHING, NOT_VISITED, VISITED };
State nodeState;
vector<PlanSys*> adjacents;
PlanSys(int x_, int y_, int r_)
{
x = x_;
y = y_;
r = r_;
depth = 0;
nodeState = State::NOT_SEARCHING;
}
};
class graph
{
public:
vector<PlanSys*> nodes;
int answer;
PlanSys* departure;
PlanSys* arrival;
graph()
{
answer = 0;
AddSys(new PlanSys(0,0,9999999));
}
void AddSys(PlanSys* psys)
{
nodes.push_back(psys);
}
void AddLink(PlanSys* a, PlanSys* b)
{
if (a == NULL || b == NULL)
{
return;
}
a->adjacents.push_back(b);
b->adjacents.push_back(a);
}
PlanSys* FindMinSys(PlanSys* psys)
{
PlanSys* minP = NULL;
for (PlanSys* p : nodes)
{
double d = distance(psys, p);
if (d < static_cast(p->r) && (minP == NULL || p->r < minP->r))
{
minP = p;
}
}
return minP;
}
void Start_BFS()
{
for (PlanSys* p : nodes)
{
p->nodeState = PlanSys::State::NOT_VISITED;
}
BFS(departure);
for (PlanSys* p : nodes)
{
p->nodeState = PlanSys::State::NOT_SEARCHING;
}
}
void BFS(PlanSys* psys)
{
queue<PlanSys*> psysQ;
psysQ.push(psys);
while (psysQ.front() != arrival)
{
psysQ.front()->nodeState = PlanSys::State::VISITED;
for (PlanSys* p : psysQ.front()->adjacents)
{
if (p->nodeState != PlanSys::State::VISITED
&& p->nodeState != PlanSys::State::NOT_SEARCHING)
{
p->depth = psysQ.front()->depth + 1;
psysQ.push(p);
}
}
psysQ.pop();
}
answer = psysQ.front()->depth;
}
double distance(PlanSys* a, PlanSys* b)
{
return sqrt(pow(a->x - b->x, 2) + pow(a->y - b->y, 2));
}
};
int main()
{
int T;
cin >> T;
for (int iter = 0; iter < T; iter++)
{
graph* g = new graph();
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
int cx, cy, r;
cin >> cx >> cy >> r;
g->AddSys(new PlanSys(cx, cy, r));
}
g->departure = g->FindMinSys(new PlanSys(x1, y1, 0));
g->arrival = g->FindMinSys(new PlanSys(x2, y2, 0));
for (int i = 1 ; i < g->nodes.size() ; i++)
{
g->AddLink(g->nodes[i], g->FindMinSys(g->nodes[i]));
}
g->Start_BFS();
cout << g->answer << endl;
}
return 0;
}
{

